Next: Project onto Spheres of Up: Extract Previous: Wave Forms Contents
Numerical Implementation
The implementation assumes that the numerical solution, on a Cartesian
grid, is approximately Schwarzshild on the spheres of constant
![]() where the waveforms are extracted. The general
procedure is then:
where the waveforms are extracted. The general
procedure is then:
- Project the required metric components, and radial derivatives
of metric components, onto spheres of constant coordinate radius
(these spheres are chosen via parameters).
- Transform the metric components and there derivatives on the
2-spheres from Cartesian coordinates into a spherical coordinate
system.
- Calculate the physical metric on these spheres if a conformal
factor is being used.
- Calculate the transformation from the coordinate radius to an
areal radius for each sphere.
- Calculate the
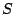 factor on each sphere. Combined with the
areal radius This also produces an estimate of the mass.
factor on each sphere. Combined with the
areal radius This also produces an estimate of the mass.
- Calculate the six Regge-Wheeler variables, and required radial
derivatives, on these spheres by integration of combinations of the
metric components over each sphere.
- Contruct the gauge invariant quantities from these
Regge-Wheeler variables.
Subsections
- Project onto Spheres of Constant Radius
- Calculate Radial Transformation
- Calculate
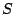 factor and Mass Estimate
factor and Mass Estimate
- Calculate Regge-Wheeler Variables
- Calculate Gauge Invariant Quantities
Next: Project onto Spheres of Up: Extract Previous: Wave Forms Contents