next up previous contents
Next: Using This Thorn Up: Numerical Implementation Previous: Calculate Regge-Wheeler Variables   Contents

Calculate Gauge Invariant Quantities


$\displaystyle Q^{\times}_{lm}$ $\textstyle =$ $\displaystyle \sqrt{\frac{2(l+2)!}{(l-2)!}}\left[c_1^{\times lm} + \frac{1}{2}\... ...{\times lm} - \frac{2}{\hat{r}} c_2^{\times lm}\right)\right] \frac{S}{\hat{r}}$ (part3128)
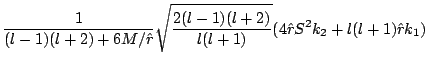$\displaystyle Q^{+}_{lm}$ $\textstyle =$ $\displaystyle \frac{1}{(l-1)(l+2)+6M/\hat{r}}\sqrt{\frac{2(l-1)(l+2)}{l(l+1)}} (4\hat{r}S^2 k_2+l(l+1)\hat{r} k_1)$ (part3129)

where
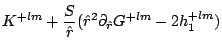$\displaystyle k_1$ $\textstyle =$ $\displaystyle K^{+lm} + \frac{S}{\hat{r}}(\hat{r}^2\partial_{\hat{r}} G^{+lm} - 2h^{+lm}_1)$ (part3130)
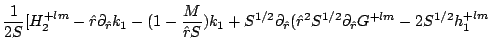$\displaystyle k_2$ $\textstyle =$ $\displaystyle \frac{1}{2S} [H^{+lm}_2-\hat{r}\partial_{\hat{r}} k_1-(1-\frac{M}... ...rtial_{\hat{r}} (\hat{r}^2 S^{1/2} \partial_{\hat{r}} G^{+lm}-2S^{1/2}h_1^{+lm}$ (part3131)