Next: Calculate factor and Mass Up: Numerical Implementation Previous: Project onto Spheres of Contents
Calculate Radial Transformation
The areal coordinate ![]() of each sphere is calculated by
of each sphere is calculated by
![\begin{displaymath}
\hat{r} = \hat{r}(r) = \left[
\frac{1}{4\pi}
\int\sqrt{\g...
...heta \theta }
\gamma_{\phi \phi }}d\theta d\phi \right]^{1/2}
\end{displaymath}](img361.png) |
(part3121) |
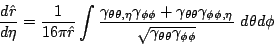 |
(part3122) |
|
Next: Calculate factor and Mass Up: Numerical Implementation Previous: Project onto Spheres of Contents Calculate Radial Transformation
The areal coordinate
|