Next: The and Invariants Up: Theoretical Background Previous: The Tetrad Contents
The Weyl Components
TheIf the tetrad has the right fall-off condition near infinity (the ``peeling property''), then the Weyl scalars
| Scalar | Falloff | Physics |
| outgoing gravitational (transverse) radiation | ||
| outgoing gauge (longitudinal) radiation | ||
| static gravitational (``Coulomb'') field | ||
| ingoing gauge (longitudinal) radiation | ||
| ingoing gravitational (transverse) radiation |
Note: This is a different convention that usually chosen.
Usually, the meanings of ![]() and
and ![]() , and of
, and of ![]() and
and
![]() are exchanged. This difference comes essentially from the
choice of the tetrad vectors
are exchanged. This difference comes essentially from the
choice of the tetrad vectors ![]() and
and ![]() ; the choice above has
; the choice above has
![]() pointing inwards and
pointing inwards and ![]() pointing outwards, which exchanges
the notion of ``outgoing'' and ``ingoing''.
pointing outwards, which exchanges
the notion of ``outgoing'' and ``ingoing''.
With a tetrad of the form (D18.1), these components
can be expressed directly in terms of spatial quantities.
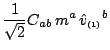 |
|||
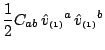 |
|||
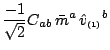 |
|||
where
Next: The and Invariants Up: Theoretical Background Previous: The Tetrad Contents