Next: Usage Up: Theoretical Background Previous: The Weyl Components Contents
The 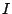 and
and 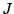 Invariants
Invariants
These are true invariants which do not depend on the choice of
coordinates or the choice of tetrad, but PsiKadelia computes them via
the 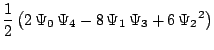 |
|||
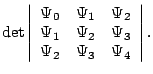 |