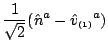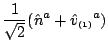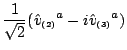The Tetrad

The tetrad is composed of two real spacetime vectors $l^a$ and $n^a$ and a complex vector $m^a$ together with its complex conjugate $\bar m^a$. PsiKadelia asumes the following $3+1$ decomposition of the tetrad:

$$l^a = \frac{1}{\sqrt 2}({\hat n}^a-\hat{v}_{\scriptscriptstyle(1)}{}^a)$$

$$n^a = \frac{1}{\sqrt 2}({\hat n}^a+\hat{v}_{\scriptscriptstyle(1)}{}^a)$$ (part381)

$$m^a = \frac{1}{\sqrt 2}({\hat{v}_{\scriptscriptstyle(2)}}{}^a-i{\hat{v}_{\scriptscriptstyle(3)}}{}^a)$$

where ${\hat n}^a$ is the unit normal to the spacelike slice, $\Sigma$, and $\hat{v}_{\scriptscriptstyle(1)}{}$, ${\hat{v}_{\scriptscriptstyle(2)}}{}$, and ${\hat{v}_{\scriptscriptstyle(3)}}{}$ are orthogonal vectors in $\Sigma$. These vectors also satisfy the normalization conditions

$$-{\hat n}^a\,{\hat n}_a=\hat{v}_{\scriptscriptstyle(1)}{}^a\... ...le(3)}}{}^a\,{\hat{v}_{\scriptscriptstyle(3)}}{}_a=1 \nonumber$$

so that the spacetime metric can be expressed as

$$g_{ab} = 2m_{(a}\bar m_{b)}-2n_{(a}l_{b)}$$

$$= \hat{v}_{\scriptscriptstyle(1)}{}_a\,\hat{v}_{\scriptscriptstyle(... ...iptstyle(3)}}{}_a\,{\hat{v}_{\scriptscriptstyle(3)}}{}_b-{\hat n}_a\,{\hat n}_b$$

In specifying a tetrad of the form (D18.1) we have reduced the number of degrees of freedom associated with the choice of orthonormal tetrad from 6 to 3. The remaining 3 degrees of freedom are fixed by specifying the directions of $\hat{v}_{\scriptscriptstyle(1)}{}^a$ and the component of ${\hat{v}_{\scriptscriptstyle(2)}}{}^a$ orthogonal to $\hat{v}_{\scriptscriptstyle(1)}{}^a$. The rest of the components of $\hat{v}_{\scriptscriptstyle(1)}{}^a$, ${\hat{v}_{\scriptscriptstyle(2)}}{}^a$, and ${\hat{v}_{\scriptscriptstyle(3)}}{}^a$ are fixed by orthonormalization.