Next: Misner Up: IDAnalyticBH Previous: Schwarzschild Contents
Kerr
Kerr initial data for an isolated rotating black hole is specified
using the ``quasi-isotropic'' coordinates [33]:
| (part327) |
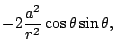 |
(part328) | ||
| (part329) | |||
| (part3210) | |||
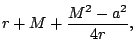 |
(part3211) | ||
| (part3212) | |||
| (part3213) |
The two free parameters are the Kerr mass,
The admbase::metric_type parameter can be used to specify
whether the metric should be conformal or not. If the metric is
conformal, then ![]() is initialised as a separate grid function, and
it's first and second derivatives are calculated analytically and also
stored as grid functions. Otherwise, the conformal factor is
multiplied through in the expression for the 3-metric before the
values of the admbase::metric variables are set. The
extrinsic curvature is also determined analytically.
is initialised as a separate grid function, and
it's first and second derivatives are calculated analytically and also
stored as grid functions. Otherwise, the conformal factor is
multiplied through in the expression for the 3-metric before the
values of the admbase::metric variables are set. The
extrinsic curvature is also determined analytically.
The gauge can be set to the Kerr lapse and shift with the parameters
idanalyticbh::initial_lapse = "kerr" idanalyticbh::initial_shift = "kerr"in which case the formulas
| (part3214) | |||
| (part3215) |
where
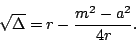 |
(part3216) |
A set of parameters which initialise an evolution to use the Kerr
intial data with mass ![]() and angular momentum
and angular momentum ![]() are:
are:
ActiveThorns = "... ADMBase StaticConformal IDAnalyticBH ..." admbase::metric_type = "static conformal" admbase::initial_data = "kerr" admbase::initial_lapse = "kerr" admbase::initial_shift = "kerr" idanalyticbh::mass = 1.0 idanalyticbh::a_kerr = 0.3
Next: Misner Up: IDAnalyticBH Previous: Schwarzschild Contents