Schwarzschild

The Schwarzschild metric corresponds to a single, static, black hole. If the Cactus metric is specified as a conformal metric (by setting admbase::metric_type="yes"), then the metric is set using isotropic coordinates [32]:

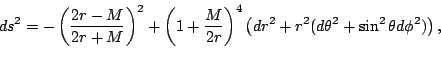$$ds^2 = -\left(\frac{2r - M}{2r + M}\right)^2 + \left(1 + \... ...^4 \left(dr^2 + r^2(d\theta^2 + \sin^2\theta d\phi^2)\right),$$ (part321)

with the Schwarzschild mass given by the single free parameter $M$. Thus, the three metric and extrinsic curvature have the values:

$$\hat{g}_{ab} = \psi^4 \delta_{ab},$$ (part322)

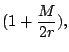$$\psi = (1 + \frac{M}{2r}),$$ (part323)

$$K_{ab} = 0.$$ (part324)

The mass is specified using the parameter idanalyticbh::mass. The black hole is assumed to reside at the origin of the grid, corresponding to the location $x=y=z=0$.

If the admbase::metric_type parameter has been set to static conformal, then the metric grid-functions (admbase::gxx, $\ldots$, admbase::gzz) are given as $\delta_{ab}$, and the conformal factor staticconformal::psi is set to the value specified above. The derivatives of the conformal factor (staticconformal::psix, etc.) are determined analytically.

In order to give the lapse an initial profile which corresponds to isotropic lapse of the $4$-metric specified above, use the parameter

  admbase::initial_lapse = "schwarz"

This will cause the admbase::alp grid-function to be initialised to the value:

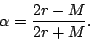$$\alpha = \frac{2r - M}{2r + M}.$$ (part325)

Note that the Schwarzschild data has the following non-standard behaviour in response to the admbase::metric_type parameter. If the physical metric is requested (ie. metric_type is set to "physical") then a different form of the Schwarzschild metric is set: Schwarzschild coordinates are set instead of the isotropic coordinates:

$$g_{xx} = g_{yy} = g_{zz} = 1 + 2M/r.$$ (part326)

In order to carry out an evolution of a single Schwarzschild black hole of mass $m=1$, using an initial lapse of $\alpha=1$, you could modify your parameter file as follows:

  ActiveThorns = "... ADMBase StaticConformal IDAnalyticBH ..."

  admbase::metric_type = "static conformal"

  admbase::initial_data = "schwarzschild"
  admbase::initial_lapse = "one"            # or "schwarz" for isotropic lapse

  idanalyticbh::mass = 1.0