- ... point.part11
- It is
possible that one may wish to modify the value of the field at the
boundary, after a physical boundary condition has already been
applied. For example, one may wish to add a small amount of noise at
the boundary to test code
stability. This added `term' is not a physical boundary condition in
itself, however, and this cannot be registered as such. To implement
such a scheme one would treat the noise in a manner similar to
symmetry boundary conditions, scheduling a routine during
BoundaryConditions (see below), after Boundary_ApplyPhysicalBCs,
which gets the list of selected variables and adds noise to their
boundaries as desired.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... variablespart12
- The consistency of the
symmetry conditions scheduled in BoundaryConditions will be
treated in an upcoming ``Symmetry'' implementation
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...part21
- If you're AMR-ing, this all refers to the
coarsest or base grid.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...part81
- Note that this means that different axes are treated
slightly differently by the interpolator. In other
words, at the level of finite differencing errors,
interpolation does not commute with permuting
the axes. However, in practice the differences are
likely to be small, at least for smooth input data.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... conditionspart101
- It is possible to alter the
calculation of L so that boundary conditions are automatically
updated and do not need setting. This is slightly tricksy. For an
example of how this would work see the new radiative boundary
condition in ADM_BSSN. For more on this see section 7.3.4
of [3].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... variablepart102
- Note that this is actually a bit of a
hack. The rational for Save and Restore variables was to deal
with maximal slicing. However it turned out that I hadn't thought it
through correctly and that the treatment for constrained variables
was required.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
cvspart201
- What is cvs? See the cvs appendix of the Users'
Guide.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... linespart202
- The BSSN_MoL thorn (in the AEIThorns
arrangement) evolves the BSSN system of equations using
the method of lines. The BSSN system uses a reparameterization
of the ADM variables
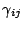 and and 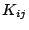 and their
evolution equations, which usually gives more stable evolutions. and their
evolution equations, which usually gives more stable evolutions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... horizonspart203
- There are also two other apparent-horizon-finder
thorns in Cactus. The TAT arrangement has the
TGRapparentHorizon2D thorn, and the AEIThorns
arrangement has the AHFinderDirect thorn. As of
late 2004, AHFinderDirect seems to be the only Cactus
apparent horizon finder which is actively maintained, and
most new work is using it.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... filespart251
- There used
to be a third, CalcTmunu_rfr.inc, which was a Cactus 3 legacy
having to do with the rfr scheduling mechanism. You may safely delete
any reference to this file.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...part331
- This slice has an apparent horizon at a
coordinate radius
 . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...part332
- See the file doc/TODO in the IDAxiBrillBH
source code for some ideas on how this might be done.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...part333
- Internally, this thorn uses ``
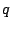 '' to refer
to '' to refer
to 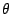 in Fortran code, with the in Fortran code, with the 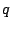 function
of function
of
 being hidden
in the Mathematica files (and not present in the Fortran
code). Noone seems to know why the code does
things this way... Unfortunately, this renaming
has leaked out into the parameter names... being hidden
in the Mathematica files (and not present in the Fortran
code). Noone seems to know why the code does
things this way... Unfortunately, this renaming
has leaked out into the parameter names...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...part334
- Notice that, for historical reasons, the
interpolation parameter names are a bit
inconsistent: interpolation_order
versus interpolator_name
and interpolator_pars.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... point.part391
- The original implementation of
these functions used a CCTK_INT8 for 64 bits, however this data type
is not supported by some Fortran compilers.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... boxpart731
-
Note that because the query is done with extreme interpolation points
coordinates, the interpolation call may fail even if all the user-supplied
interpolation points are well within each processor's local patch.
The reason for this implementation behaviour is that we safely want to catch
all errors caused by a too small ghostzone size.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...CCTK_InterpGridArrays()part732
- In C the return code is the CCTK_InterpGridArrays() function result; in Fortran it's returned through
the first (status) argument.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... HDF5part781
- Hierarchical Data
Format version 5, see http://hdf.ncsa.uiuc.edu/whatishdf5.html for details
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... normspart951
- We use both RMS-norms and
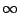 -norms.
We define the RMS-norm of a set of -norms.
We define the RMS-norm of a set of 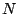 numbers numbers
 is defined to be the square root of
their mean square, is defined to be the square root of
their mean square,
 . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... epsilonpart952
- ``Machine epsilon''
 is defined to be the smallest positive
floating-point number such that is defined to be the smallest positive
floating-point number such that
 compares ``not equal to'' 1.0 in floating-point
arithmetic. Machine epsilon values can be found
in the standard header file <float.h>;
for IEEE single and double precision they are
about
compares ``not equal to'' 1.0 in floating-point
arithmetic. Machine epsilon values can be found
in the standard header file <float.h>;
for IEEE single and double precision they are
about
 and and
 respectively.
respectively.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
|
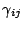 and
and 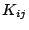 and their
evolution equations, which usually gives more stable evolutions.
and their
evolution equations, which usually gives more stable evolutions.
 .
.
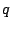 '' to refer
to
'' to refer
to 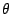 in Fortran code, with the
in Fortran code, with the 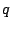 function
of
function
of
 being hidden
in the Mathematica files (and not present in the Fortran
code). Noone seems to know why the code does
things this way... Unfortunately, this renaming
has leaked out into the parameter names...
being hidden
in the Mathematica files (and not present in the Fortran
code). Noone seems to know why the code does
things this way... Unfortunately, this renaming
has leaked out into the parameter names...
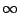 -norms.
We define the RMS-norm of a set of
-norms.
We define the RMS-norm of a set of 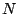 numbers
numbers
 is defined to be the square root of
their mean square,
is defined to be the square root of
their mean square,
 .
.
 is defined to be the smallest positive
floating-point number such that
is defined to be the smallest positive
floating-point number such that
 compares ``not equal to'' 1.0 in floating-point
arithmetic. Machine epsilon values can be found
in the standard header file <float.h>;
for IEEE single and double precision they are
about
compares ``not equal to'' 1.0 in floating-point
arithmetic. Machine epsilon values can be found
in the standard header file <float.h>;
for IEEE single and double precision they are
about
 and
and
 respectively.
respectively.