When is a Test Result ``Ok''?

All other things being equal, we can't expect any of our error norms^part951 to be any smaller than a few times machine epsilon^part952 for the floating-point type in question. Moreover, if we're taking $n$th derivatives in the interpolation, then since we're dividing by $1/(\Delta\!x)^n$ in the computation, the error norms will typically be a factor of $1/(\Delta\!x)^n$ larger than they would be if no derivatives were being taken.

To aid in judging the test results, we thus also print a set of ``scaled error norms'', where each ``raw'' error norm is divided by its ``minimum plausible'' value $\epsilon /(\Delta\!x)^n$.

We specify a set of 4 scaled error norm thresholds as parameters to the test driver, a ``low'' and a ``high'' threshold for each of the RMS-norm and $\infty$-norm scaled error norms. Finally, we classify the outcome of each test as follows:

ok

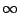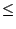if both the RMS-norm and the $\infty$-norm scaled errors are $\le$ their ``low'' thresholds.

marginal

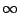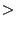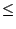if at least one of the RMS-norm and the $\infty$-norm scaled errors are $>$ their ``low'' thresholds, but both are still $\le$ their ``high'' thresholds.

FAIL

if either of the RMS-norm and the 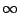$\infty$-norm scaled errors are 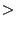$>$ their ``high'' thresholds.

The makefiles in the run/* directories print a summary of the number of ok/marginal/FAIL tests run for each target (``1d'', ``2d'', or ``3d''). (Alas, there's no ``master summary'' done across all numbers of dimensions.)