Generating Initial Data with IDBrillData

Brill initial data is activated by choosing the CactusEinstein/ADMBase parameter initial_data to be brilldata, or for the case of axisymmetry brilldata2D can also be used.

The parameter IDBrillData::q_function chooses the form of the $q$ function to be used, defaulting to the Gundlach expression.

Additional IDBrillData parameters for each form of $q$ fix the remaining freedom:

• Exponential 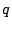$q$: IDBrillData::q_function = "exp"

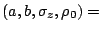  $(a, b,\sigma_z,\rho_0)=$ (exp_a, exp_b, exp_sigmaz,exp_rho0)

• Eppley 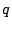$q$: IDBrillData::q_function = "eppley"

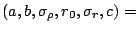  $(a, b,\sigma_\rho, r_0,\sigma_r,c)=$ (eppley_a, eppley_b, eppley_sigmarho, eppley_r0, eppley_sigmar, eppley_c)

• Gundlach 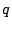$q$: IDBrillData::q_function = "gundlach"

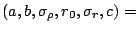  $(a, b,\sigma_\rho, r_0,\sigma_r,c)=$ (gundlach_a, gundlach_b, gundlach_sigmarho, gundlach_r0, gundlach_sigmar, gundlach_c)

• Non-axisymmetric part for each choice of $q$

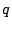
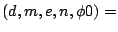  $(d, m, e, n, \phi0)=$ (brill3d_d, brill3d_m, brill3d_e, brill3d_n, brill3d_phi0)

Note that the default $q$ expression is

$$q = {\tt gundlach\_a} \quad \rho^2 e^{-r^2}$$

IDBrillData can use the elliptic solvers (type LinMetric) provided by CactusEinstein/EllSOR,
AEIThorns/BAM_Elliptic, or CactusElliptic/EllPETSc to solve the equation resulting from the Hamiltonian constraint. In all cases the parameter thresh sets the threshold for the elliptic solve. The choice of elliptic solver is made through the parameter brill_solver:

• sor: Understands the Robin boundary condition, additional parameters control the maximum number of iterations (sor_maxit).

• bam: BAM_Elliptic does not properly implement the elliptic infrastructure of EllBase, and the BAM_Elliptic parameter to use the Robin boundary condition must be set independently of
  IDBrillWave::brill_bound.