Purpose

The purpose of this thorn is to create (time symmetric) initial data for a Brill wave spacetime. It does so by starting from a three-metric of the form originally considered by Brill

$$ds^2 = \Psi^4 \left[ e^{2q} \left( d\rho^2 + dz^2 \right) + \rho^2 d\phi^2 \right] =\Psi^4 \hat{ds}^{2},$$ (part341)

where $q$ is a free function subject to certain regularity and fall-off conditions, $\rho=\sqrt{x^2+y^2}$ and $\Psi$ is a conformal factor to be solved for.

Thorn IDBrillData provides three choices for the $q$ function: an exponential form, (IDBrillData::q_function = "exp")

$$q = a \; \frac{\rho^{2+b}}{r^2} e^{-\left( \frac{z}{\sigma_z... ...m}{1 + e \rho^m} \cos^2 \left( n \phi + \phi_0 \right) \right]$$ (part342)

a generalized form of the $q$ function first written down by Eppley (IDBrillData::q_function = "eppley")

$$q = a \left( \frac{\rho}{\sigma_\rho} \right)^b \frac{1}{1 +... ...m}{1 + e \rho^m} \cos^2 \left( n \phi + \phi_0 \right) \right]$$ (part343)

and the (default) Gundlach $q$ function which includes the Holz form (IDBrillData::q_function = "gundlach")

$$q = a \left( \frac{\rho}{\sigma_\rho} \right)^b e^{-\left[ \... ...m}{1 + e \rho^m} \cos^2 \left( n \phi + \phi_0 \right) \right]$$ (part344)

Substituting the metric into the Hamiltonian constraint gives an elliptic equation for the conformal factor $\Psi$ which is then numerically solved for a given function $q$:

$$\hat{\nabla} \Psi - \frac{\Psi}{8} \hat{R} = 0$$ (part345)

where the conformal Ricci scalar is found to be

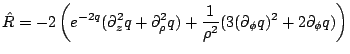$$\hat{R} = -2 \left(e^{-2q} (\partial^2_z q + \partial^2_\rho q) + \frac{1}{\rho^2} (3 (\partial_\phi q)^2 + 2 \partial_\phi q)\right)$$ (part346)

Assuming the initial data to be time symmetric means that the momentum constraints are trivially satisfied.

In the case of axisymmetry (that is $d=0$ in the above expressions for $q$), the Hamiltonian constraint can be written as an elliptic equation for $\Psi$ with just the flat space Laplacian,

$$\nabla_{flat} \Psi + \frac{\Psi}{4} (\partial_z^2 q + \partial_\rho^2 q) = 0$$ (part347)

If the initial data is chosen to be ADMBase::initial_data = "brilldata2D" then this elliptic equation is solved rather than the equation above.