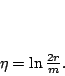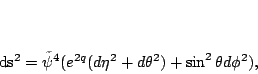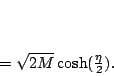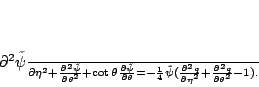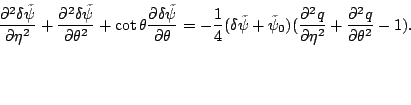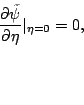


Next: The Resulting Slice
Up: IDAxiBrillBH
Previous: Abstract
Contents
The pioneer, Bernstein, studied a single black hole which is
non-rotating and distorted in azimuthal line symmetry of 2 dimensional
case [37]. In this non-rotating case, one chooses the
condition,  , and , and
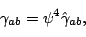 |
(part331) |
where 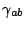 is the physical three metric and is the physical three metric and
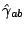 is some chosen conformal three metric. is some chosen conformal three metric.
The Hamiltonian constraint reduces to
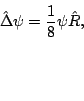 |
(part332) |
where 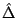 is the covariant Laplacian and is the covariant Laplacian and 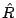 is the
Ricci tensor for the conformal three metric. This form allows
us to choose an arbitrary conformal three metric, and then solve an
elliptic equation for the conformal factor, therefore satisfying the
constraint equations ( is the
Ricci tensor for the conformal three metric. This form allows
us to choose an arbitrary conformal three metric, and then solve an
elliptic equation for the conformal factor, therefore satisfying the
constraint equations (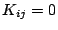 trivially satisfies the momentum
constraints in vacuum). This approach was used to create
``Brill waves'' in a spacetime without black holes [38].
Bernstein extended this to the black hole spacetime. Using
spherical-polar coordinates, one can write the 3-metric, trivially satisfies the momentum
constraints in vacuum). This approach was used to create
``Brill waves'' in a spacetime without black holes [38].
Bernstein extended this to the black hole spacetime. Using
spherical-polar coordinates, one can write the 3-metric,
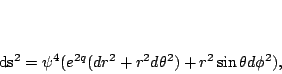 |
(part333) |
where 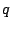 is the Brill ``packet'' which takes some functional form.
Using this ansatz with (D13.2)
leads to an elliptic equation for is the Brill ``packet'' which takes some functional form.
Using this ansatz with (D13.2)
leads to an elliptic equation for 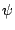 which must be solved
numerically. Applying the isometry condition on which must be solved
numerically. Applying the isometry condition on 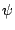 at a finite
radius, and applying at a finite
radius, and applying 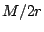 falloff conditions on falloff conditions on 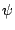 at the
outer boundary (the ``Robin'' condition), along with a packet which
obeys the appropriate symmetries (including being invariant under the
isometry operator), will make this solution describe a black hole with
an incident gravitational wave. The choice of at the
outer boundary (the ``Robin'' condition), along with a packet which
obeys the appropriate symmetries (including being invariant under the
isometry operator), will make this solution describe a black hole with
an incident gravitational wave. The choice of 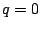 produces the
Schwarzschild solution. The typical produces the
Schwarzschild solution. The typical 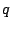 function used in
axisymmetry, and considered here in the non-rotating case, is function used in
axisymmetry, and considered here in the non-rotating case, is
![\begin{displaymath}
q = Q_0 \sin^n \theta \left [ \exp\left(\frac{\eta -
\eta...
... \exp\left(\frac{\eta +
\eta_0^2}{\sigma^2}\right ) \right ].
\end{displaymath}](img451.png) |
(part334) |
Note regularity along the axis requires that the exponent 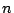 must be
even. Choosing a logarithmic radial coordinate must be
even. Choosing a logarithmic radial coordinate
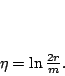 |
(part335) |
(where 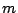 is a scale parameter), one can rewrite
(D13.3) as is a scale parameter), one can rewrite
(D13.3) as
![\begin{displaymath}
ds^2 = \psi(\eta)^4 [ e^{2 q} (d \eta^2 + d\theta^2) + \sin^2
\theta d\phi^2].
\end{displaymath}](img454.png) |
(part336) |
The scale parameter 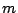 is equal to the mass of the Schwarzschild
black hole, if is equal to the mass of the Schwarzschild
black hole, if 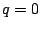 . In this coordinate, the 3-metric is . In this coordinate, the 3-metric is
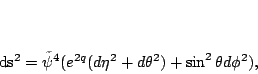 |
(part337) |
and the Schwarzschild solution is
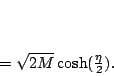 |
(part338) |
We also change the notation of 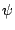 for the conformal factor is same
as for the conformal factor is same
as 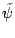 [39], for the [39], for the 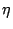 coordinate has the
factor coordinate has the
factor 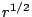 in the conformal factor. Clearly in the conformal factor. Clearly 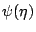 and and
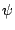 differ by a factor of differ by a factor of 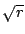 . The Hamiltonian
constraint is . The Hamiltonian
constraint is
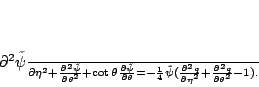 |
(part339) |
For solving this Hamiltonian constraint numerically. At first
we substitute
to the equation (D13.9), then we can linearize it as
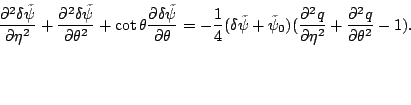 |
(part3312) |
For the boundary conditions, we use for the inner boundary condition
an isometry condition:
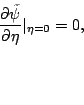 |
(part3313) |
and outer boundary condition, a Robin condition:
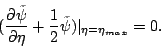 |
(part3314) |



Next: The Resulting Slice
Up: IDAxiBrillBH
Previous: Abstract
Contents
|
![]() , and
, and
![]() is equal to the mass of the Schwarzschild
black hole, if
is equal to the mass of the Schwarzschild
black hole, if ![]() . In this coordinate, the 3-metric is
. In this coordinate, the 3-metric is
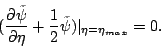
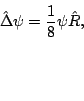
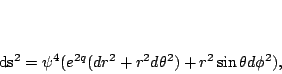
![\begin{displaymath}
q = Q_0 \sin^n \theta \left [ \exp\left(\frac{\eta -
\eta...
... \exp\left(\frac{\eta +
\eta_0^2}{\sigma^2}\right ) \right ].
\end{displaymath}](img451.png)