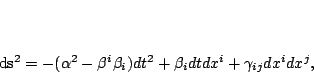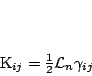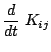


Next: Parameters
Up: ADM
Previous: Abstract
Contents
This thorn evolves the standard ADM equations, see [7]. The
line element is
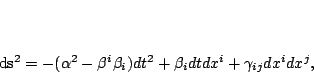 |
(part211) |
where 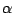 is the lapse, is the lapse, 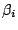 the shift vector and the shift vector and
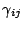 the 3-metric. Defining the 3-metric. Defining 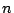 to be the normal to the
slice, we have the extrinsic curvature to be the normal to the
slice, we have the extrinsic curvature 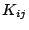 given by given by
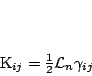 |
(part212) |
where 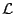 is the Lie derivative. is the Lie derivative.
The ADM equations then evolve the spatial three metric 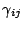 and the extrinsic curvature
and the extrinsic curvature 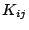 using using
with
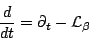 |
(part215) |
and where
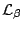 is the Lie derivative with respect to the
shift vector is the Lie derivative with respect to the
shift vector 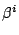 . Here . Here 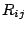 is the Ricci tensor and is the Ricci tensor and 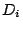 the covariant derivative associated with the three-dimensional metric
the covariant derivative associated with the three-dimensional metric
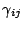 . The 4-dimensional Ricci tensor . The 4-dimensional Ricci tensor
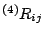 is
usually written in terms of the energy density is
usually written in terms of the energy density 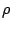 and stress
tensor and stress
tensor 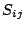 of the matter as seen by the normal (Eulerian) observers: of the matter as seen by the normal (Eulerian) observers:
![\begin{displaymath}
{}^{(4)}R_{ij} = 8 \pi \left[ S_{ij} - \frac{1}{2} \left( S - \rho
\right) \right] .
\end{displaymath}](img223.png) |
(part216) |



Next: Parameters
Up: ADM
Previous: Abstract
Contents
|
![]() and the extrinsic curvature
and the extrinsic curvature ![]() using
using
![\begin{displaymath}
{}^{(4)}R_{ij} = 8 \pi \left[ S_{ij} - \frac{1}{2} \left( S - \rho
\right) \right] .
\end{displaymath}](img223.png)