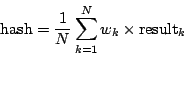Next: Running the Tests Up: TestInterp Previous: Test Functions Contents
Output Files
Once the interpolation is done, TestInterp prints various error norms to standard output, and can optionally produce 3 main types of output file:
- We can print any single interpolation result in detail, in
a generic ASCII format which can be inspected by hand or
ploted with gnuplot or other graphics programs. This is
controlled by the
plot_output_typeandplot_file_nameparameters. - We can print the Jacobian of the interpolation (as obtained
by querying the interpolator, as estimated by numerical perturbations,
or both) to a data file, again in a generic ASCII format which
is convenient for gnuplot. This is controlled by the
print_Jacobian_fileandJacobian_file_nameparameters. - For a Cactus test suite, both of the previous options are a bit
inconvenient because they produce fairly large output files
for 3-D interpolation, and because they attempt to write
the same output files on each processor of a multiprocessor
run. (This latter point is really a bug.)
Instead, for test-suite purposes, we can also ``hash''
all the interpolation results of a given Cactus data type
down into a single number (this makes the test-suite data
files nice and small!), check that this is identical
on each processor of a multiprocessor run, and (only on
processor #0) write this to a data file. This is controlled
by the
print_hash_files,hash_difference_file_name,hash_data_file_name_real,hash_data_file_name_real4, andhash_data_file_name_real8parameters.The ``hashing'' here is really just a linear combination
where the weights
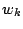 are chosen to be pseudorandom numbers
fairly close to unity, typically in the range
are chosen to be pseudorandom numbers
fairly close to unity, typically in the range 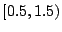 .
This definition has the properties that
.
This definition has the properties that
- the hash is a continuous (in fact linear) function of the interpolation results
- the Jacobian of the hash with respect to any given result is reasonably close to unity
- if the hash matches the archived value for a test suite,
then it's highly likely that all the individual interpolation
results also matched their archived values (i.e. it's
highly unlikely that the errors in the different interpolation
results just happened to cancel out in the linear
combination
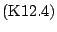 ).
).
![]()
![]()
![]()
![]()
Next: Running the Tests
Up: TestInterp
Previous: Test Functions
Contents