Test Functions

This thorn supports several different types of ``smooth functions'':

xy

A simple test function with a single (2nd order) off-axis term:

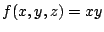
$$f(x,y,z) = xy$$ (part951)

generic

This is a ``generic'' trancendental test function which should have all terms nonzero in its Taylor series:

$$f(x,y,z) = \tanh\Big[ \sin\Big( x + \arctan\big[y-\cos(z)+0.314\big] \Big) \Big]$$

$$\quad \times \arctan\Big[ \cos\Big( y - \tan\big[z+\sin(x)-0.159\big] \Big) \Big]$$

$$\quad \times \cos\Big[ \arctan\Big( z + \sin\big[x-\tanh(y)+0.265\big] \Big) \Big] <tex2html_comment_mark>$$ (part952)

series

This is probably the most useful test function. It has all possible terms in its Taylor expansion up to a specified order,

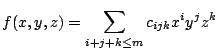
$$f(x,y,z) = \sum_{i+j+k \le m} c_{ijk} x^i y^j z^k$$ (part953)

where the maximum order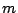 $m$ may be any integer between 1 and 6 inclusive. The series coefficients 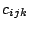$c_{ijk}$ are chosen to be pseudorandom numbers in the range [0,1). (A different set of series coefficients is used for each different Cactus data type to be tested.) For testing differentiating interpolators, TestInterp also knows how to compute all possible 1st and 2nd partial derivatives of this test function.