EllBase Programming Guide

Here we give a step by step guide on how to implement an new elliptic solver class, its interface and provide a solver for this class. Since some of the functionality needed in the registration code can only be achieved in C, a basic knowledge of C is helpful.

• Assumption:
  • The elliptic equation class will be called ``SimpleEllClass'': it will be flat space solver, that only takes the coefficient matrix 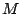$M$: Note that this solver class is already provided by EllBase.
  • The name of the demonstration thorn will be ``ThornFastSOR''. Since I will only demonstrate the registration principle and calling structure, I leave it to the interested reader to write a really fast SOR solver.
  • The solver for this elliptic equation will be called ``FastSOR_solver'' and will be written in Fortran. Since Fortran cannot be called directly by the registration mechanism, we need to have C wrapper function ``FastSOR_wrapper''.

• Elliptic class declaration: SimpleEllThorn/src/SimpleEll_Class.c

• Elliptic solver interface: src/SimpleEll_Interface.c

  #include ``cctk.h''
  #include ``cctk_Parameters.h''
  
  #include ``cctk_FortranString.h'' 
  #include ``StoreNamedData.h''
  
  static pNamedData *SimpleEllSolverDB;
  
  void Ell_SimpleEllSolverRegistry(void (*solver_func), const char *solver_name)
  {
    StoreNamedData(&SimpleEllSolverDB,solver_name,(void*)solver_func);
  }
  

  The routine above registers the solver (or better the function pointer of the solver routine ``*solve_func'') for the equation class SimpleEllClass by the name solver_name in the database SimpleEllSolverDB. This database is declared in statement static pNamedData....

  Next, we write our interface in the same file ./SimpleEll_Interface.c:

  void Ell_SimpleEllSolver(cGH *GH, int *FieldIndex, int *MIndex, 
  		         CCTK_REAL *AbsTol, CCTK_REAL *RelTol,
                           const char *solver_name) {
  
  /* prototype for the equation class wrapper:
     grid hierarchy(*GH), ID-number of field to solve for (*FieldIndex),
     two arrays of size three holding convergence information (*AbsTol, *RelTol)
  */
    void (*fn)(cGH *GH, int *FieldIndex, int *AbsTol, int *RelTol);
  
    /* derive the function name from the requested name and hope it is there */
    fn = (void(*)) GetNamedData(LinConfMetricSolverDB,solver_name);
    if (!fn) CCTK_WARN(0,''Ell_SimpleEllSolver: Cannot find solver! ``);
  
    /* Now that we have the function pointer to our solver, call the 
       solver and pass through all the necessary arguments */
    fn( GH, FieldIndex, MIndex, AbsTol, RelTol);
  }
  

  The interface Ell_SimpleEllSolver is called from the user side. It receives a pointer to the grid hierarchy, the ID-number of the field to solver for, two arrays which the used upload with convergence test info, and finally, the name of the solver the user want to employ *solver_name. Note: all these quantities are referenced by pointers, hence the ``*''.

  Within the interface, the solver_name is used to get the pointer to function which was registered under this name. Once the function is known, it called with all the arguments passed to the interface.

  To allow calls from Fortran, the interface in C needs to be ``wrapped''. (This wrapping is different from the one necessary to make to actual solver accessible by the elliptic registry).

  /* Fortran wrapper for the routine Ell_SimpleEllSolver */
  void CCTK_FCALL CCTK_FNAME(Ell_SimpelEllSolver)
       (cGH *GH, int *FieldIndex, int *MIndex, 
       int *AbsTol, int *RelTol, ONE_FORTSTRING_ARG) {
    ONE_FORTSTRING_CREATE(solver_name);
  
    /* Call the interface */
    Ell_SimpleEllSolver(GH, FieldIndex, MIndex, AbsTol, RelTol, solver_name);
    free(solver_name);
  }
  

• Elliptic solver:./src/FastSOR_solver.F
  Here we show the first lines of the Fortran code for the solver:

        subroutine FastSOR_solver(_CCTK_ARGUMENTS,
       .   Mlinear_lsh,Mlinear, 
       .   var,
       .   abstol,reltol)
  
        implicit none
  
        _DECLARE_CCTK_ARGUMENTS
        DECLARE_CCTK_PARAMETERS
        INTEGER CCTK_Equals
  
        INTEGER Mlinear_lsh(3)
        CCTK_REAL Mlinear(Mlinear_lsh(1),Mlinear_lsh(2),Mlinear_lsh(3))
        CCTK_REAL var(cctk_lsh(1),cctk_lsh(2),cctk_lsh(3))
  	
        INTEGER Mlinear_storage
  
  c     We have no storage for M if they are of size one in each direction
        if ((Mlinear_lsh(1).eq.1) .and. 
       .   (Mlinear_lsh(2).eq.1)  .and.
       .   (Mlinear_lsh(3).eq.1)) then
           Mlinear_storage=0
        else
           Mlinear_storage=1
        endif
  

  This Fortran solver receives the following arguments: the ``typical'' CCTK_ARGUMENTS: _CCTK_ARGUMENTS, the size of the coefficient matrix: Mlinear_lsh, the coefficient matrix Mlinear, the variable to solve for: var, and the two arrays with convergence information.

  In the declaration section, we declare: the cctk arguments, the Mlinear size array, the coefficient matrix, by the 3-dim. size array, the variable to solve for. Why do we pass the size of Mlinear explicitly and do not use the cctk_lsh (processor local shape of a grid function) as we did for var ? The reason is the following: while we can expect the storage of var to be on for the solve, there is no reason (in a more general elliptic case) to assume, that the coefficient matrix has storage allocated, perhaps it is not needed at all! In this case, we have to protect ourself against referencing empty arrays. For this reason, we also employ the flag Mlinear_storage.

• Elliptic solver wrapper:./src/FastSOR_wrapper.c
  The Fortran solver can not be used within the elliptic registry directly. Instead the Fortran code is called through a wrapper:

  void FastSOR_wrapper(cGH *GH, int *FieldIndex, int *MIndex, 
  		     int *AbsTol,int *RelTol) {
  
    CCTK_REAL *Mlinear=NULL, *var=NULL;
    int Mlinear_lsh[3];
    int i;
  
    var = (CCTK_REAL*) CCTK_VarDataPtrI(GH,0,*FieldIndex);
  
    if (*MIndex>0) Mlinear   = (CCTK_REAL*) CCTK_VarDataPtrI(GH,0,*MIndex);
  
  
    if (GH->cctk_dim>3)
      CCTK_WARN(0,''This elliptic solver implementation does not do dimension>3!'');  
    
    for (i=0;i<GH->cctk_dim;i++) {
      if((*MIndex<0))  Mlinear_lsh[i]=1;
      else             Mlinear_lsh[i]=GH->cctk_lsh[i];
    }
  
    /* call the fortran routine */
    CCTK_FNAME(SimpleEll_Solver)(_PASS_CCTK_C2F(GH),
           Mlinear_lsh, Mlinear, var, 	
  	 AbsTol, RelTol);
  }
  

  The wrapper FastSOR_wrapper takes these arguments: the indices of the field to solve for (FieldIndex) and the coefficient matrix (MIndex), the two arrays containing convergence information (AbsTol, RelTol). In the body of the program we provide two CCTK_REAL pointers to the data section of the field to solver (var, Mlinear) by means of Get_VarDataPtrI. For Mlinear, we only do this, if the index is non-negative. A negative index is a signal by the user that the coefficient matrix has no storage allocated.(For more general elliptic equation cases, e.g. no source terms.) To make this information of a possibly empty matrix available to Fortran, we load a 3-dim. and pass this array through to Fortran. See discussion above.

• Elliptic solver startup: ./src/Startup.c
  The routine below in Startup.c performs the registration of our solver wrapper FastSOR_wrapper under the name ``fastsor'' for the elliptic class ``Ell_SimpleEll''. We do not register with the solver interface Ell_SimpleEllSolver directly, but with the class. In Startup,c we have:

  #include ``cctk.h''
  #include ``cctk_Parameters.h''
  
  void FastSOR_register(cGH *GH) {
  
    /* protoype of the solver wrapper: */
    void FastSOR_wrapper(cGH *GH, int *FieldIndex, int *MIndex,
                        	int *AbsTol, int*RelTol);
  
    Ell_RegisterSolver(FastSOR_wrapper,''fastsor'',''Ell_SimpleEll'');
  }
  

  Note that more solver registration code could be put here (registration for other classes, etc.)

• Elliptic solver scheduling: schedule.ccl We schedule the registration of the fast SOR solver at CCTK_BASE, by this time, the elliptic class Ell_SimpleEll has already been registered.

  schedule FastSOR_register at CCTK_INITIAL
  {
    LANG:C
  } ``Register the fast sor solver''