Next: Extending the elliptic solver Up: Solving an elliptic equation Previous: Ell_LinMetric Contents
Ell_LinConfMetric
To call this interface from Fortran:call Ell_LinMetricSolver(ierr, cctkGH, MetricPsi_gfi, . phi_gfi, M_gfi, N_gfi, . AbsTol, RelTol, "solvername")To call this interface from C:
ierr = Ell_LinMetricSolver(GH, MetricPsi_gfi, phi_gfi, M_gfi, N_gfi, AbsTol, RelTol, "solvername");Argument List:
- ierr: return value: ``0'' success
- cctkGH: the Fortran ``pointer'' to the grid function hierachy.
- GH: the C pointer to the grid hierarchy, type: pGH *GH
- MetricPsi_gfi: array of size
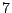 , containing the grid function index of the metric components and the grid
function index of the conformal factor
, containing the grid function index of the metric components and the grid
function index of the conformal factor 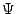 :
:  ,
,
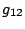 ,
, 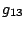 ,
, 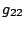 ,
, 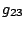 ,
, 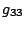 ,
, 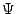 . The order is important.
. The order is important.
- phi_gif: the integer index of the grid function so solver for.
- M_gfi: the integer index of the grid function which holds
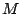 .
.
- N_gif: the integer index of the grid function which holds
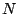
- AbsTol: array of size
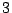 : holding absolute tolerance values for the
: holding absolute tolerance values for the
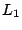 ,
, 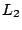 ,
, 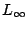 Norm. Check, if the solver side supports
these norms.The interface side does not guarantee that these norms are
actually implemenented by a solver. See the section on Norms: E1.7.
Norm. Check, if the solver side supports
these norms.The interface side does not guarantee that these norms are
actually implemenented by a solver. See the section on Norms: E1.7.
- RelTol: array of size
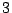 : holding relative
tolerance factors for the
: holding relative
tolerance factors for the 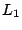 ,
, 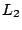 ,
, 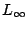 . Check, if the
solver side supports these norms. The interface side does not
guarantee that these norms are actually implemenented by a solver.
See the section on Norms: E1.7.
. Check, if the
solver side supports these norms. The interface side does not
guarantee that these norms are actually implemenented by a solver.
See the section on Norms: E1.7.
- "solvername": the name of a solver, which is registered
for a particular equation class. How to find out the names ? Either
check the documentation of the elliptic solvers or check for
registration infomation outputted by a cactus at runtime.
Next: Extending the elliptic solver Up: Solving an elliptic equation Previous: Ell_LinMetric Contents