Purpose of the thorn

This thorn integrates timelike geodesics. The integration is done on the fly, that is, at the same time as the evolution of the spacetime is being calculated. The thorn can calculate geodesics either on the numerical spacetime, or on an exact spacetime (given by thorn Exact).

`num_active:`	Integration of geodesics on numerical spacetime [yes,no].
`num_test:`	Tests of geodesic integration on numerical spacetime [yes,no].
`num_IJ:`	Calculate invariants and on numerical spacetime [yes,no].
	`Yes` option requires thorn: PsiKadelia. (This should probably be changed to Zorro?)
`exa_active:`	Integration of geodesics on exact spacetime [yes,no]. `Yes` option requires thorn: Exact.
`exa_IJ:`	Calculate invariants I and J on exact spacetime [yes,no].

The fundamental variables used are the position of the geodesics and the covariant components of the momentum. The reason for using the covariant components of the momentum as fundamental variables instead of the more natural contravariant components is that the geodesic equations become in fact much simpler this way, and all time derivatives of the metric drop out.

The initial number of geodesics is determined by the value of the parameter ngeos.

The initial positions of the geodesics are determined by the values of the parameter geopos:

`geopos = x00:`	Uniform distribution along x axis.
`geopos = 0y0:`	Uniform distribution along y axis.
`geopos = 00z:`	Uniform distribution along z axis.
`geopos = xy0:`	Uniform distribution along xy diagonal.
`geopos = x0z:`	Uniform distribution along xz diagonal.
`geopos = 0yz:`	Uniform distribution along yz diagonal.
`geopos = xyz:`	Uniform distribution along xyz diagonal.
`geopos = grid:`	Uniform 3D down-sampled distribution.
	The down sampling factor should be given using the parameter `geo_sample`.

I also choose the initial geodesics to point in the normal direction to the hypersurfaces. This can be easily changed if someone really needs it.

For the numerical spacetime, I use coordinate time as the parameter, and I integrate proper time along the geodesics. The form of the equations used is: ( $\alpha$ = lapse, $\beta$ = shift, $\gamma$ = 3-metric,

= position,

= momentum)

$\displaystyle \frac{dx^i}{dt}$	$\textstyle =$	$\displaystyle - \beta^i + \gamma^{ik}\frac{p_k}{p^0}$	(part411)
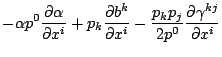$\displaystyle \frac{dp_i}{dt}$	$\textstyle =$	$\displaystyle -\alpha p^0 \frac{\partial \alpha}{\partial x^i} + p_k \frac{\par... ...{\partial x^i} - \frac{p_k p_j}{2 p^0}\frac{\partial \gamma^{kj}}{\partial x^i}$
$\displaystyle \frac{d\tau}{dt}$	$\textstyle =$	$\displaystyle \frac{1}{p^0}$

$\begin{displaymath} p^0 = \frac{1}{\alpha} \sqrt{1 + \gamma^{kj} p_k p_j} \end{displaymath}$

(part412)

For the exact spacetime, I use proper time as the parameter. This is because I don't know which exact coordinate time corresponds to a given numerical coordinate time (the solutions might be on different gauges). The form of the equations is then slightly different from those given above (there is an extra factor P0):

$\displaystyle \frac{dx^i}{d\tau}$	$\textstyle =$	$\displaystyle - \beta^i p^0 + \gamma^{ik}p_k$	(part413)
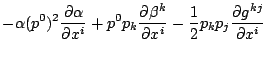$\displaystyle \frac{dp_i}{d\tau}$	$\textstyle =$	$\displaystyle -\alpha (p^0)^2 \frac{\partial \alpha}{\partial x^i} + p^0 p_k \f... ...beta^k}{\partial x^i} - \frac{1}{2}p_k p_j \frac{\partial g^{kj}}{\partial x^i}$