Psi Minus Two

The psiminustwo choice of initial lapse sets

$$\alpha = \left(\frac{1-2s+s\psi}{\psi-s}\right)^2$$

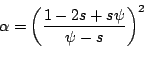
The cut off value $s$ (parameter psiminustwo_cut must lie between zero and one. If $s=0$ then $\alpha=1/\psi^2$, while if $s=1$ then $\alpha=1$. This gauge choice can only be used with metric_type = "static conformal".

This choice of lapse was originally implemented as an experiment to improve the initial profile of the lapse for $1+\log$ slicing (see the documentation for the ADM or BSSN thorns). This condition is not elliptic, and the effect of the collapse of the lapse around the singularities propagates outward with a finite gauge speed, resulting in a visible ``kink'' in the lapse function. For data such as the Brandt-Brügmann puncture data, the psiminustwo lapse falls off asymptotically in the same way as maximal slicing, and already posesses the collapse feature at the puncture, and thus is a potentially useful initial profile for puncture-type evolutions.