Two-throat Misner data

The misner_bh initial data generates a metric of the form

$$ds^2 = -dt^2 + \psi^4 (dx^2 + dy^2 + dz^2),$$ (part3217)

where the conformal factor $\psi$ is given by

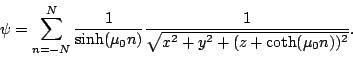$$\psi = \sum^N_{n=-N} \frac{1}{\sinh(\mu_0 n)} \frac{1}{\sqrt{x^2 + y^2 + (z + \coth(\mu_0 n))^2}}.$$ (part3218)

The extrinsic curvature for the Misner data is zero.

The parameter $\mu _0$ is a measure of the ratio of mass to separation of the throats, and is set using the parameter idanalyticbh::mu. For values less than $\mu\simeq 1.8$, the throats will have a single event horizon.

The summation limit $N$ can be set using the parameter idanalyticbh::nmax. Ideally, it should tend to infinity, but in practice the default value of $N=30$ works well enough for the applications that have been tested. The misner_nbh parameter is only used for the multiple_misner_bh multi-throat data, and will be ignored for the misner_bh initial data, which assumes two throats.

For the given metric, the ADM mass of the system is determined via

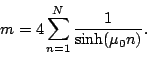$$m = 4 \sum^N_{n=1} \frac{1}{\sinh(\mu_0 n)}.$$ (part3219)

This quantity is determined automatically and written to standard output.

If the conformal form of the metric is used (via the admbase::metric_type parameter), then derivatives of the conformal factor are computed analytically from the derivatives of the above expression for $\psi$.

To make use of the two black hole initial data, a variation of the following set of parameters can be used:

  ActiveThorns = "... ADMBase StaticConformal IDAnalyticBH ..."

  admbase::metric_type = "static conformal"

  admbase::initial_data = "misner_bh"
  idanalyticbh::mu = 2.2