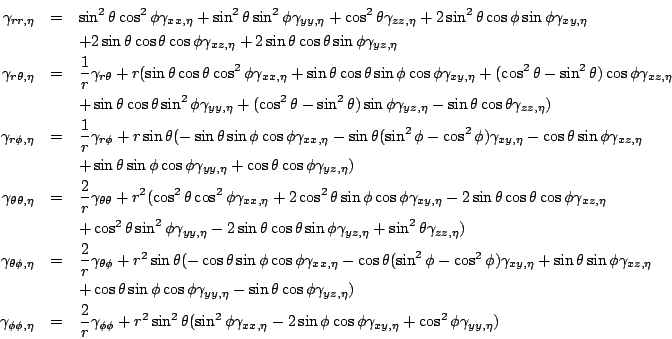Next: Appendix: Integrations Over the Up: Extract Previous: Appendix: Regge-Wheeler Harmonics Contents
Appendix: Transformation Between Cartesian and Spherical Coordinates
First, the transformations between metric components in ![]() and
and
![]() coordinates. Here,
coordinates. Here,
![]() ,
,
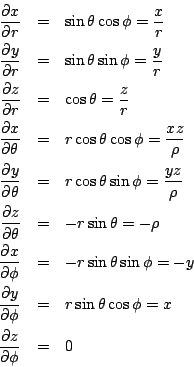
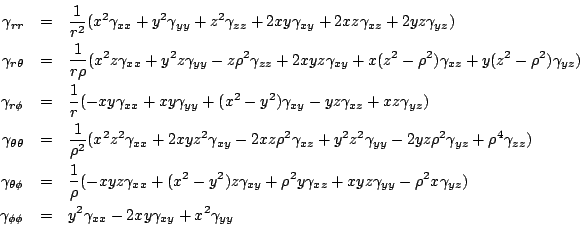
or,
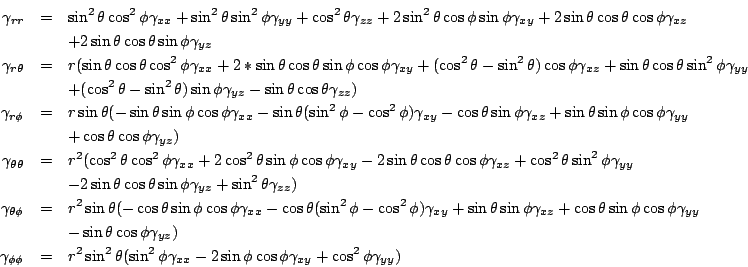
We also need the transformation for the radial derivative of the metric components: