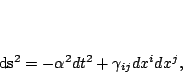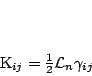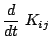Next: Using This Thorn Up: EvolSimple Previous: Abstract Contents
Physical System
The line element is
where
The ADM equations then evolve the spatial three metric ![]() and the extrinsic curvature
and the extrinsic curvature ![]() using
using
with
| (part305) |
Next: Using This Thorn Up: EvolSimple Previous: Abstract Contents