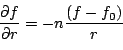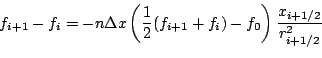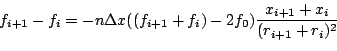


Next: Additional arguments
Up: Boundary
Previous: Calling from Fortran:
Contents
This boundary condition has not yet been implemented in
individual coordinate directions.
The Robin boundary condition is:
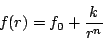 |
(part14) |
with 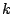 a constant, a constant, 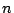 the decay rate and the decay rate and 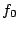 the value at infinity. This implies: the value at infinity. This implies:
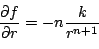 |
(part15) |
or
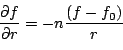 |
(part16) |
Considering now a given Cartesian direction 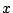 we get: we get:
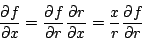 |
(part17) |
which implies
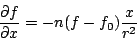 |
(part18) |
The equations are then finite differenced around the grid point 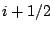 : :
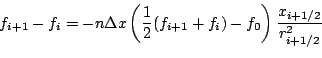 |
(part19) |
or
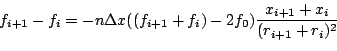 |
(part110) |
And this is then solved either for 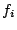 or or 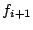 depending on which side are
we looking at. depending on which side are
we looking at.
The Robin boundary condition is registered under the name ``Robin''.
Subsections



Next: Additional arguments
Up: Boundary
Previous: Calling from Fortran:
Contents
|