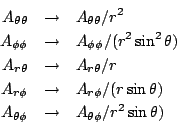Next: Computing the Ricci tensor Up: ADMAnalysis Previous: Determinant of 3-Metric Contents
Transformation to Spherical Cooordinates
The values of the metric and/or extrinsic curvature in a spherical
polar coordinate system
![]() evaluated at each point on
the computational grid are placed in the grid functions (grr,
grt, grp, gtt, gtp, gpp) and (krr,
krt, krp, ktt, ktp, kpp).
In the spherical transformation, the
evaluated at each point on
the computational grid are placed in the grid functions (grr,
grt, grp, gtt, gtp, gpp) and (krr,
krt, krp, ktt, ktp, kpp).
In the spherical transformation, the ![]() coordinate is referred to
as q and the
coordinate is referred to
as q and the ![]() as p.
as p.
The general transformation from Cartesian to Spherical for such tensors is
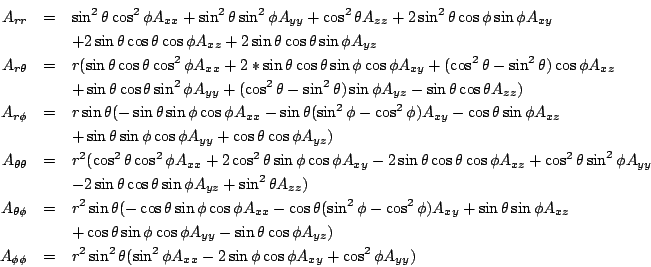
If the parameter normalize_dtheta_dphi is set to yes,
the angular components are projected onto the vectors
![]() instead of the default vector
instead of the default vector
![]() . That is,
. That is,