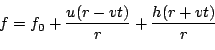Next: Additional arguments Up: Boundary Previous: Arguments Contents
Radiation Boundary Condition
This is a two level scheme. Grid functions are given for the current time level (to which the BC is applied) as well as grid functions from a past timelevel which are needed for constructing the boundary condition. The grid function of the past time level needs to have the same geometry. Currently radiative boundary conditions can only be applied with a stencil width of one in each direction.
The radiative boundary condition that is implemented is
Condition A1.1 above leads to the differential equation:
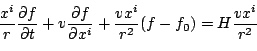 |
(part12) |
At a given boundary only the derivatives in the normal direction are
considered. Notice that ![]() has disappeared, but we still do
not know the value of
has disappeared, but we still do
not know the value of ![]() .
.
To get ![]() we do the following: The expression is evaluated one
point in from the boundary and solved for
we do the following: The expression is evaluated one
point in from the boundary and solved for ![]() there. Now we need a way of
extrapolating
there. Now we need a way of
extrapolating ![]() to the boundary. For this, assume that
to the boundary. For this, assume that
![]() falls off as a power law:
falls off as a power law:
| (part13) |
The observed behavior is the following: Using ![]() is very stable, but has a very bad initial transient. Taking
is very stable, but has a very bad initial transient. Taking
![]() to be 0 or positive improves the initial behavior considerably,
but introduces a drift that can kill an evolution at very late
times. Empirically, the best value found so far is
to be 0 or positive improves the initial behavior considerably,
but introduces a drift that can kill an evolution at very late
times. Empirically, the best value found so far is ![]() , for
which the initial behavior is very nice, and the late time drift
is quite small.
, for
which the initial behavior is very nice, and the late time drift
is quite small.
Another problem with this condition is that it does not
use the physical characteristic speed, but rather it assumes
a wave speed of ![]() , so the boundaries should be out in
the region where the characteristic speed is constant.
Notice that this speed does not have to be 1.
, so the boundaries should be out in
the region where the characteristic speed is constant.
Notice that this speed does not have to be 1.
The radiation boundary condition is registered under the name ``Radiation''.
Subsections
Next: Additional arguments Up: Boundary Previous: Arguments Contents