Description

Thorn Time uses one of four methods to decide on the timestep to be used for the simulation. The method is chosen using the keyword parameter time::timestep_method.

• time::timestep_method = "given"

  The timestep is fixed to the value of the parameter time::timestep.

• time::timestep_method = "courant_static"

  This is the default method, which calculates the timestep once at the start of the simulation, based on a simple courant type condition using the spatial gridsizes and the parameter time::dtfac.
  

  $$\Delta t = \mbox{\tt dtfac} * \mbox{min}(\Delta x^i)$$
  
  
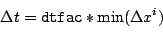
  Note that it is up to the user to custom dtfac to take into account the dimension of the space being used, and the wave speed.

• time::timestep_method = "courant_speed"

  This choice implements a dynamic courant type condition, the timestep being set before each iteration using the spatial dimension of the grid, the spatial grid sizes, the parameter courant_fac and the grid variable courant_wave_speed. The algorithm used is
  

  $$\Delta t = \mbox{\tt courant\_fac} * \mbox{min}(\Delta x^i)/\mbox{\tt courant\_wave\_speed}/\sqrt{\mbox dim}$$
  
  
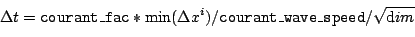
  For this algorithm to be successful, the variable courant_wave_speed must have been set by some thorn to the maximum propagation speed on the grid before this thorn sets the timestep, that is AT POSTSTEP BEFORE Time_Courant (or earlier in the evolution loop). [Note: The name courant_wave_speed was poorly chosen here, the required speed is the maximum propagation speed on the grid which may be larger than the maximum wave speed (for example with a shock wave in hydrodynamics, also it is possible to have propagation without waves as with a pure advection equation).

• time::timestep_method = "courant_time"

  This choice is similar to the method courant_speed above, in implementing a dynamic timestep. However the timestep is chosen using
  

  $$\Delta t = \mbox{\tt courant\_fac} * \mbox{\tt courant\_min\_time}/\sqrt{\mbox dim}$$
  
  
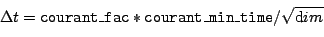
  where the grid variable courant_min_time must be set by some thorn to the minimum time for a wave to cross a gridzone before this thorn sets the timestep, that is AT POSTSTEP BEFORE Time_Courant (or earlier in the evolution loop).

In all cases, Thorn Time sets the Cactus variable cctk_delta_time which is passed as part of the macro CCTK_ARGUMENTS to thorns called by the scheduler.

Note that for hyperbolic problems, the Courant condition gives a minimum requirement for stability, namely that the numerical domain of dependency must encompass the physical domain of dependency, or

$$\Delta t \le \mbox{min}(\Delta x^i)/\mbox{wave speed}/\sqrt{\mbox dim}$$