Next: Example Tensor Type Declarations Up: SymBase Previous: Driver Interaction Contents
Tensor Types
Cactus supports declaring the tensor type of grid function groups. These tensor types define how the grid functions, which are supposed to be tensor components, transform under various transformations, such as reflections and rotations.
The tensor types are not declared directly; instead, a tensor type alias is declared. The following tensor type aliases are currently known and supported:
- scalar:
- a scalar
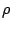
- u:
- a vector
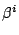
- d:
- a covector
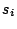
- dd_sym:
- a symmetric rank two tensor
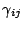
In addition to the tensor type, one can also declare the tensor
parity, tensor weight, and a tensor metric. The
tensor parity (an integer) specifies the behaviour under reflections.
Scalars and polar vectors have a parity ![]() , pseudo scalars and axial
vectors have a parity
, pseudo scalars and axial
vectors have a parity ![]() . The tensor weight (a real number)
specifies the behaviour under transformations that change the volume
element. The tensor metric (a string) specifies what metric has to be
used to raise or lower indices for that quantity.
. The tensor weight (a real number)
specifies the behaviour under transformations that change the volume
element. The tensor metric (a string) specifies what metric has to be
used to raise or lower indices for that quantity.
Last but not least, a tensor special can be defined for quantities that do not transform as tensor. The currently supported tensor specials are
- Gamma:
- for the transformation behaviour of the
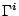 variables of the
BSSN formalism; it is
variables of the
BSSN formalism; it is
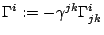 with
with
- log:
- for the transformation behaviour of the variable
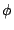 of the BSSN
formalism; it is
of the BSSN
formalism; it is
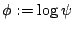 with
with
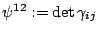 .
.
By default, the basis with respect to which the tensor components are given is supposed to be the (local) coordinate system given by the grid, i.e., the coordinate directions are the ``natural'' directions of the grid. It is possible to specify a different basis by declaring a tensor basis, which is the name of a grid function group containing the coordinate system.
Subsections
Next: Example Tensor Type Declarations Up: SymBase Previous: Driver Interaction Contents