Next: Interaction With Symmetry Conditions Up: SymBase Previous: Querying Symmetries of Faces Contents
Symmetry Interpolation
The mechanism by which the grid points are mapped into the domain works as follows:
- The user calls CCTK_InterpGridArrays with a list of coordinates.
- The Flesh forwards this call to the driver.
- The driver calls SymBase's aliased function, SymmetryInterpolate, passing along all arguments.
- SymBase sets a flag for each face for which a symmetry condition has been registered, and then calls SymmetryInterpolateFaces, passing along all arguments. This is the beginning of a chain of recursive calls.
- SymmetryInterpolateFaces checks whether any faces are flagged.
- If no faces are flagged, SymBase calls the driver's aliased function DriverInterpolate, which performs the actual interpolation. This ends the chain of recursive calls.
- If there are faces with symmetry conditions flagged, SymBase chooses one such face, and then calls the ``symmetry interpolation'' routine of the symmetry condition registered for this face, passing along all arguments.
- The ``symmetry interpolation'' routine maps the coordinates into the domain by applying the symmetry condition for this face. It then removes the flag for the corresponding face, and calls SymmetryInterpolateFaces, passing along the arguments with the changed interpolation locations.
- After the actual interpolation has happened in the driver, the
recursive call will return. The ``symmetry interpolation'' routine
then examines the tensor types of the interpolated quantities and
un-maps the values back onto their original locations. That is,
e.g., after a reflection on the lower
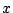 -boundary,
-boundary, 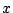 -components
of vectors need their sign changed.
-components
of vectors need their sign changed.
- The chain of recursive calls unravels until the call to CCTK_InterpGridArrays returns.
|
[scale=.833,clip=true]/home/cactus_web/CheckOut/CactusStable/arrangements/CactusBase/SymBase/doc/fig/recursion
|
This mechanism has thus four players:
- The driver forwards any CCTK_InterpGridArrays call to SymBase SymmetryInterpolate so that the list of interpolation points can be mapped into the domain. (See section A11.6.2.)
- Thorn SymBase controls which symmetry conditions perform this mapping on which faces.
- Each symmetry boundary condition has to register a ``symmetry interpolation'' routine that first maps the points into the domain, then calls SymBase SymmetryInterpolateFaces recursively. Before returning, it performs the inverse coordinate transformation on the interpolated quantities.
- The user calls CCTK_InterpGridArrays. For them the rest of the mechanism is transparent.
Subsections
Next: Interaction With Symmetry Conditions Up: SymBase Previous: Querying Symmetries of Faces Contents