Basic Reduction Operations

The following reduction operations are imlemented. $a_i$ are the values that are reduced, $i \in [1 \ldots n]$.

count:

The number of values

$$\mathrm{count} := n$$

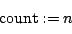
sum:

The sum of the values

$$\mathrm{sum} := \sum_i a_i$$

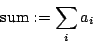
product:

The product of the values

$$\mathrm{product} := \prod_i a_i$$

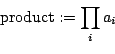
sum2:

The sum of the squares of the values

$$\mathrm{sum2} := \sum_i a_i^2$$

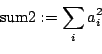
sumabs:

The sum of the absolute values

$$\mathrm{sum2} := \sum_i \vert a_i\vert$$

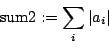
sumabs2:

The sum of the squares of the absolute values

$$\mathrm{sumabs2} := \sum_i \vert a_i\vert^2$$

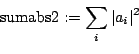
min:

The minimum of the values

$$\mathrm{min} := \min_i a_i$$

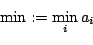
max:

The maximum of the values

$$\mathrm{max} := \max_i a_i$$

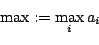
maxabs:

The maximum of the absolute values

$$\mathrm{maxabs} := \max_i \vert a_i\vert$$

Note that the above definitions are for both real and complex values. For $n=0$, the result of the reduction operation is $0$, except for $\mathrm{product}$, which is $1$, $\mathrm{min}$, which is $+\infty$, and $\mathrm{max}$, which is $-\infty$. We define the minimum of complex values by

$$\min \left( a+ib, x+iy \right) := \min \left( a,x \right) + i \min \left (b,y \right)$$

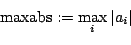
and define the maximum equivalently.